 The first time that I visited Ivor Darreg (in 1981) he was living in Glendale, California. I was impressed by his amazing array of experimental instruments, but what grabbed me most was his re-fretted guitars. He had a large collection of them, guitars that he had carefully altered over the years. There were so many that it was a veritable feast to me! I had never played re-fretted guitars before, and it was almost overwhelming. Many of his guitars were pretty trashy – Ivor was not a wealthy man, but his dedication to the exploration of alternative tunings was quite impressive. A handful of them were pretty good – I think that I played all of them for a few minutes that unforgettable day. He had guitars in 19-ET, 22-ET, quarter-tone, 17-ET, and other odd divisions, but the sweetness of the 31-ET guitar impressed me most. It was also right at the `edge’ of the possible, or so it seemed to me. There were so many frets, so close together, how could you possibly put more frets on a guitar? Some years later I played a 34-ET guitar, and it largely confirmed the sentiment. From that day forward, I had an interest in 31-ET guitars.
The first time that I visited Ivor Darreg (in 1981) he was living in Glendale, California. I was impressed by his amazing array of experimental instruments, but what grabbed me most was his re-fretted guitars. He had a large collection of them, guitars that he had carefully altered over the years. There were so many that it was a veritable feast to me! I had never played re-fretted guitars before, and it was almost overwhelming. Many of his guitars were pretty trashy – Ivor was not a wealthy man, but his dedication to the exploration of alternative tunings was quite impressive. A handful of them were pretty good – I think that I played all of them for a few minutes that unforgettable day. He had guitars in 19-ET, 22-ET, quarter-tone, 17-ET, and other odd divisions, but the sweetness of the 31-ET guitar impressed me most. It was also right at the `edge’ of the possible, or so it seemed to me. There were so many frets, so close together, how could you possibly put more frets on a guitar? Some years later I played a 34-ET guitar, and it largely confirmed the sentiment. From that day forward, I had an interest in 31-ET guitars.
Although I could `noodle’ my way around the fretboard, I soon found that it was almost impossible to play because I would invariably get lost. What fret am I on, and what chord is this? I then realized that the problem could be solved if some colour-cocle would be painted onto the neck for visual guidance. Ivor had a colour-code (rather complex) for his megalyra steel-guitar, but his `normal’ guitars were generally unmarked. On standard guitars, we generally use an inlay dot at the 5th, 7th, and 12th frets as the `colour-code’, and arguably this is adequate for 12-ET, but 31-ET is so complex (rich) that this traditional system no longer proves adequate. I began several years of experiment with alternative colour-codes trying to come up with an optimal design.
In fact, I caught the `guitar-altering bug’ from Ivor, and when I was back in Canada I acquired a semi-trashy electric guitar which seemed perfect for `experimentation’. (What is there to lose?) I had never done a guitar fret job before, so I assumed that the results would be pretty bad. To my surprise, the scale turned out to be pretty close to accurate, there was only a minimum of `buzzes’, and I now had my own 31-ET guitar! At this point, my irnerest in colour-codes intensified. By 1984, I had several designs which arguably have some consistent logic underlying them. The purpose of this little article is to lay out the reasons for my chosen design. Here is why I ended up with this particular pattern.
Click on the link to see the article in your browser or right-click to save the file to your drive.
http://siementerpstra.com/writings/Terpstra-Fretboards.pdf
 The Dictionary of Harmonic Functions endeavours to lay out the materials (interval relations, harmonic patterns) for the 12-E.T. tuning system in an elegant as well as practical manner. The relative simplicity of the tuning system, as opposed to the more complex musical cycles of 31 or 53, makes such an inventory manageable. Moreover, the 12 cycle is not dependant on a layout involving the matrix associated with the more complex cycles. Unlike the 19, 31, 43, and 53 cycles which are Prime, the 12 cycle is a Composite System, donating special properties to this much-used framework.
The Dictionary of Harmonic Functions endeavours to lay out the materials (interval relations, harmonic patterns) for the 12-E.T. tuning system in an elegant as well as practical manner. The relative simplicity of the tuning system, as opposed to the more complex musical cycles of 31 or 53, makes such an inventory manageable. Moreover, the 12 cycle is not dependant on a layout involving the matrix associated with the more complex cycles. Unlike the 19, 31, 43, and 53 cycles which are Prime, the 12 cycle is a Composite System, donating special properties to this much-used framework.

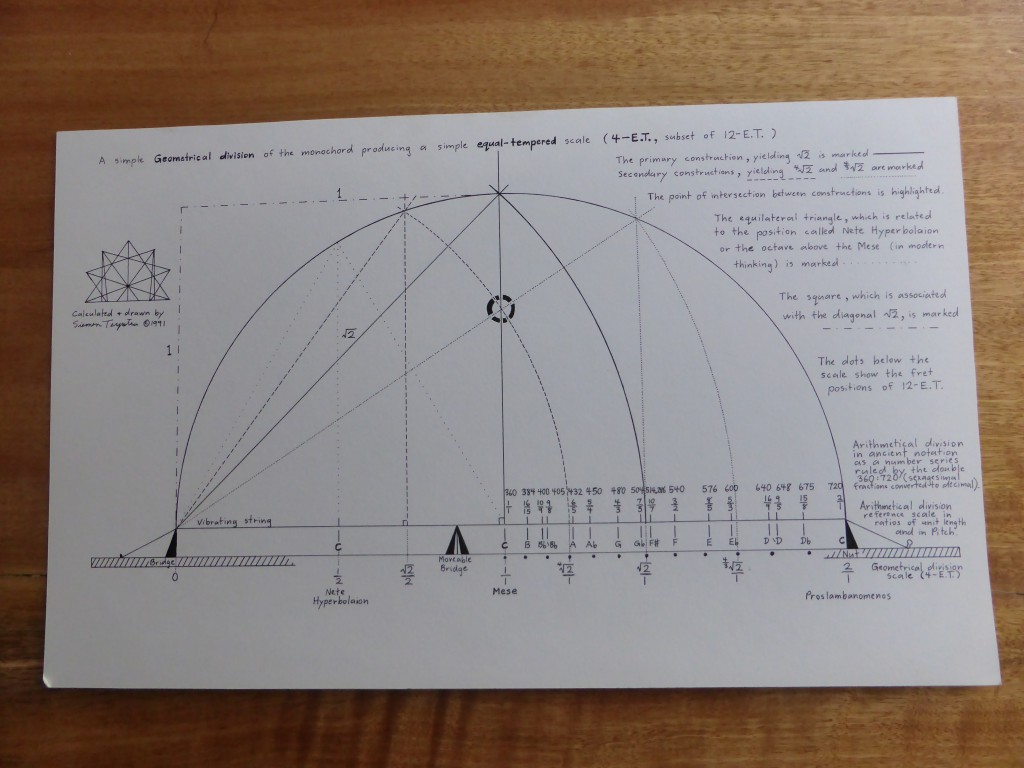
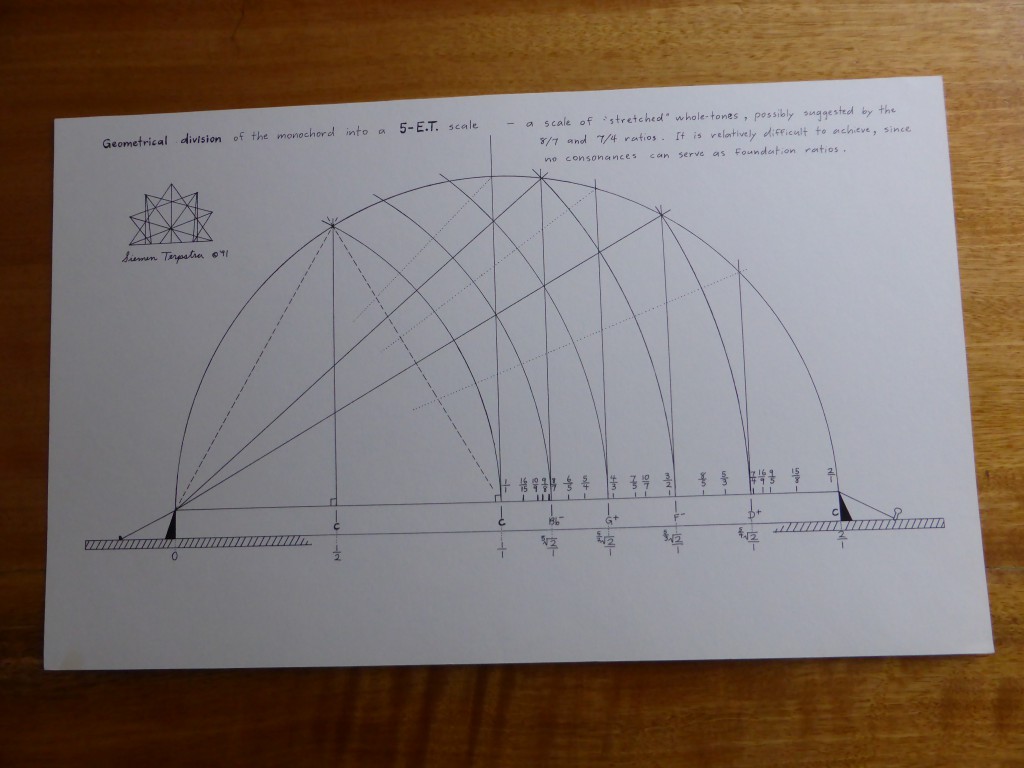
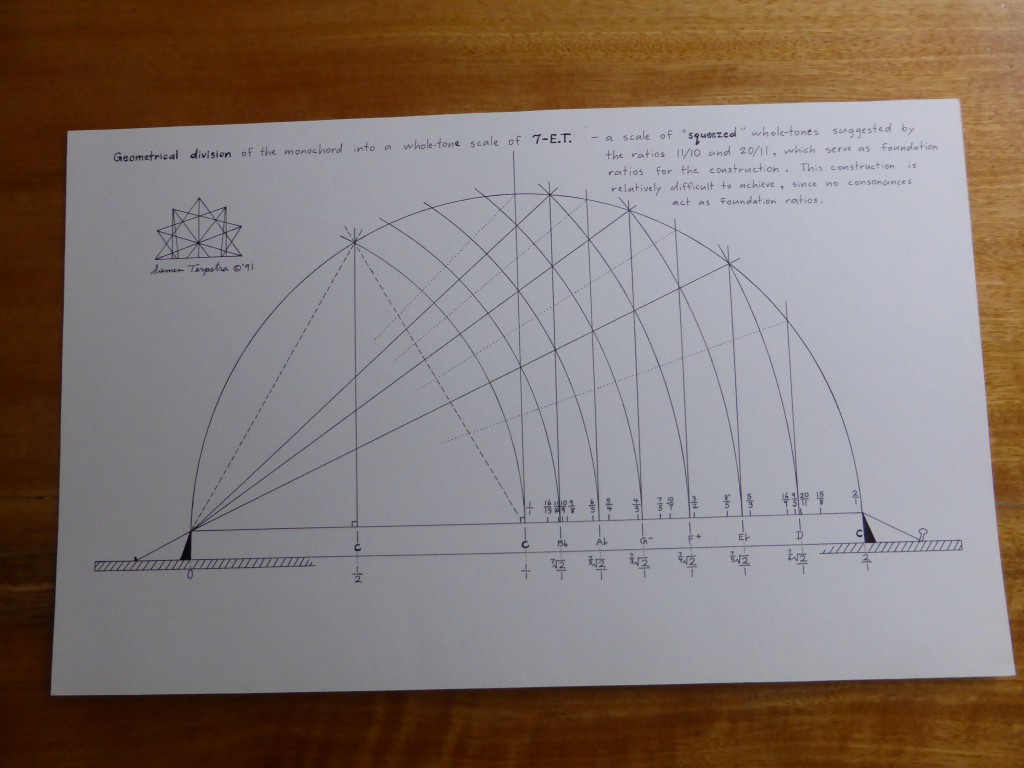
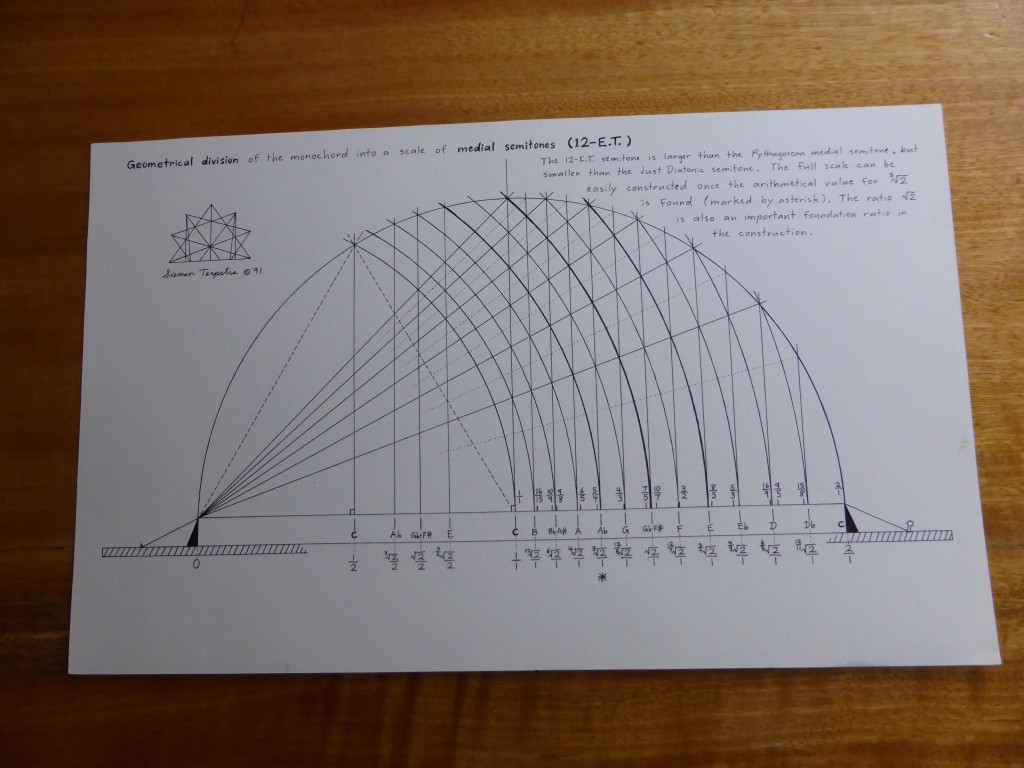
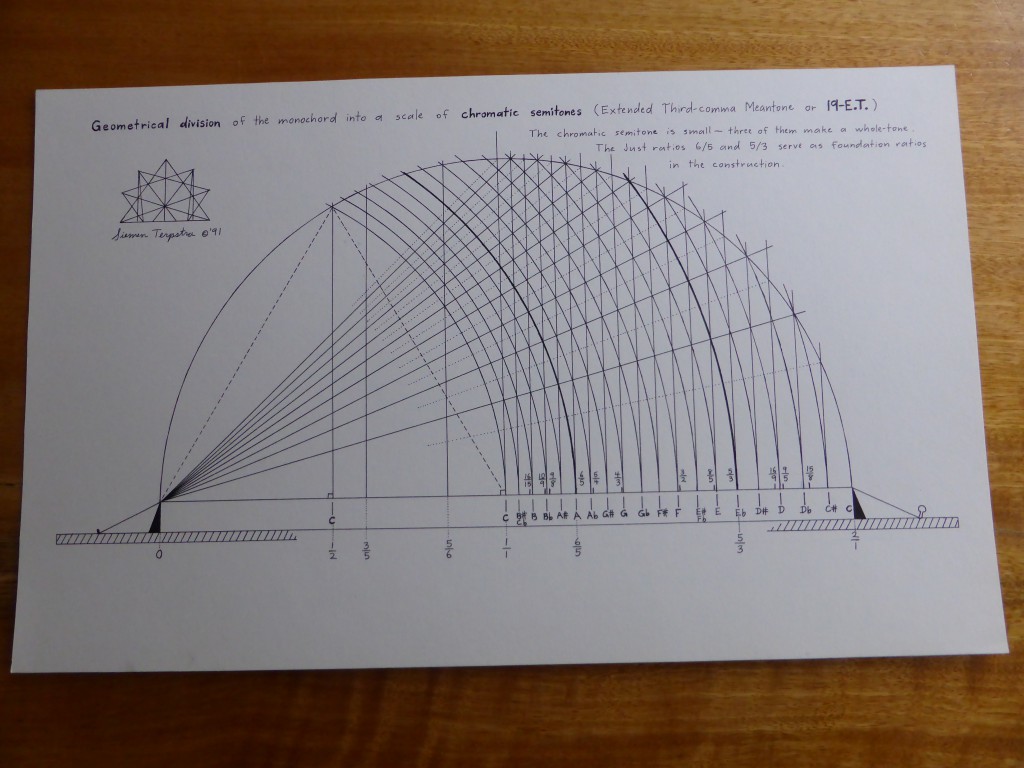
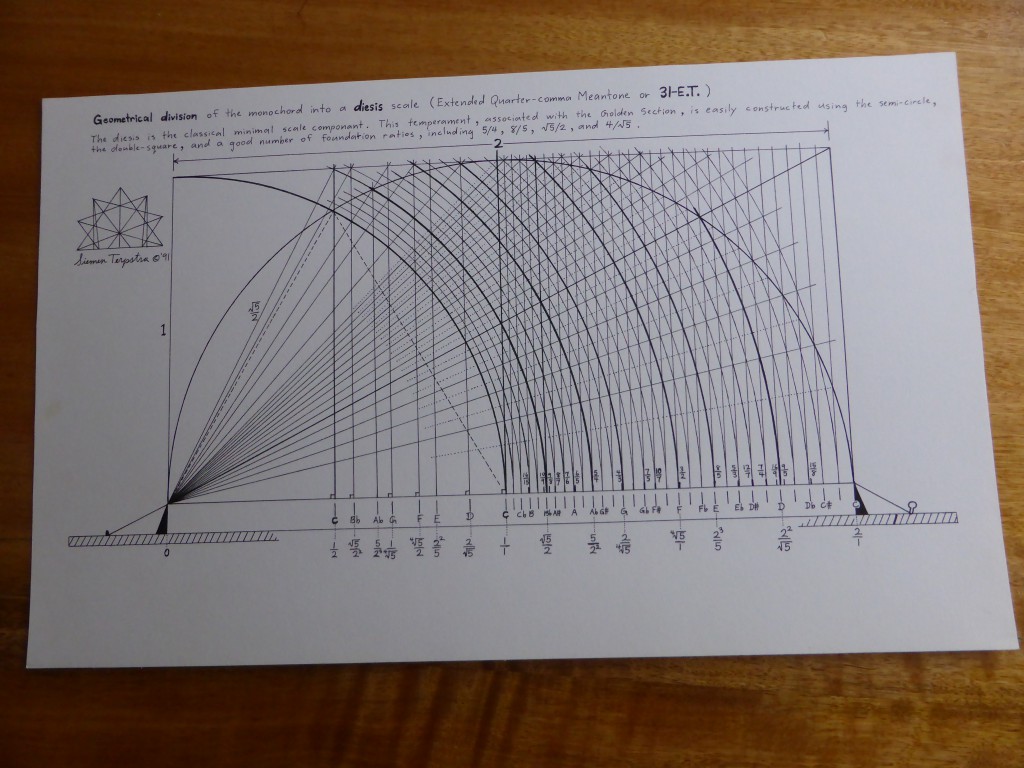
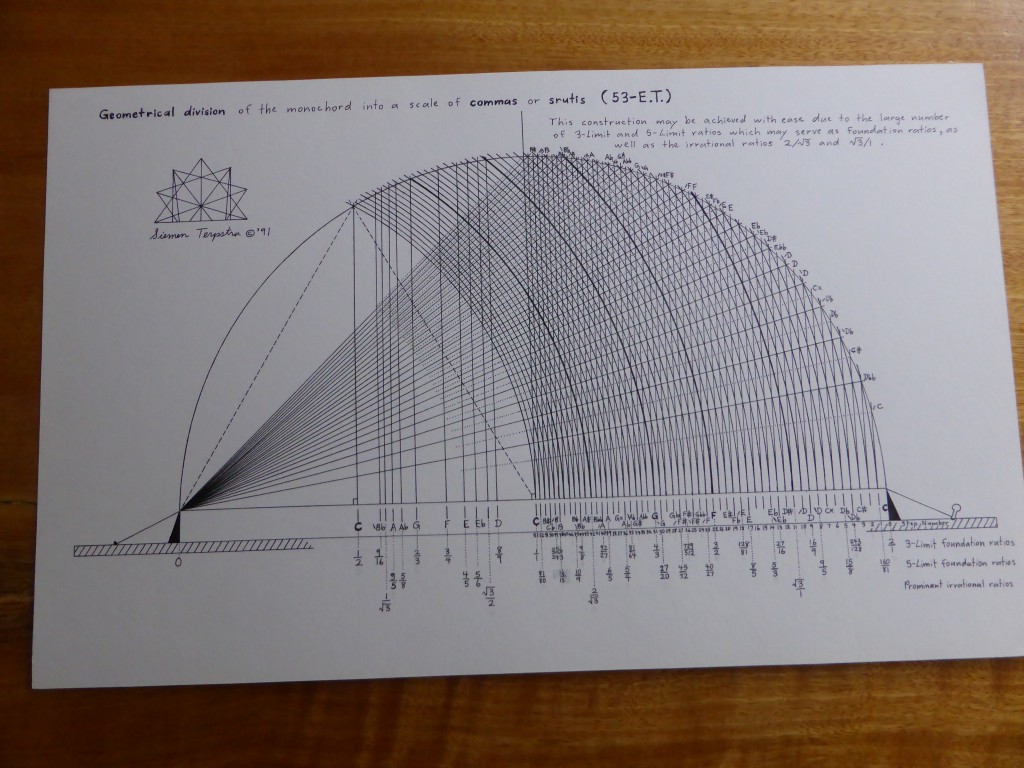
 The first time that I visited
The first time that I visited  The GLOBAL KEYBOARDS refer to a complimentary pair of generalized musical typewriters for computer-based electronic media. Since the design was formulated in 1986 it has been given several names: the Spectrum Keyboards (after a discarded color scheme), the One-Circle Global Keyboards (after an essential parameter of the design), or just my generalized keyboards. The complimentary relation between the two keyboards has also led me to call them male and female.
The GLOBAL KEYBOARDS refer to a complimentary pair of generalized musical typewriters for computer-based electronic media. Since the design was formulated in 1986 it has been given several names: the Spectrum Keyboards (after a discarded color scheme), the One-Circle Global Keyboards (after an essential parameter of the design), or just my generalized keyboards. The complimentary relation between the two keyboards has also led me to call them male and female. I was asked to evaluate 37 notation proposals by the committee of the MNMA. I examined all the proposals and gave their strong and weak points. Then I chose the six best and further narrowed it down to two alternatives. It was published by the MNMA in 1999.
I was asked to evaluate 37 notation proposals by the committee of the MNMA. I examined all the proposals and gave their strong and weak points. Then I chose the six best and further narrowed it down to two alternatives. It was published by the MNMA in 1999. The author examines an interesting and neglected set of harmonies that make up the diminished scale. Along the way he demonstrates the usefulness of the Expansion Index as an organisational tool. In addition, he makes some introductory remarks concerning the comparative musical theory of tonal harmony.
The author examines an interesting and neglected set of harmonies that make up the diminished scale. Along the way he demonstrates the usefulness of the Expansion Index as an organisational tool. In addition, he makes some introductory remarks concerning the comparative musical theory of tonal harmony. The author looks at a variety of substitutions for V7 and IVm6 within tonal harmony and why such procedures work. Meanwhile he explores some fundamental issues of music theory.
The author looks at a variety of substitutions for V7 and IVm6 within tonal harmony and why such procedures work. Meanwhile he explores some fundamental issues of music theory. The author examines a variety of chord progressions within tonal harmony. In order to better understand the syntax or ‘flow’ he defends a morphological toll called the Reciprocity Model of chord progression. With this aid he looks at some interesting features mainly oriented around the extended meantone fabric of harmony.
The author examines a variety of chord progressions within tonal harmony. In order to better understand the syntax or ‘flow’ he defends a morphological toll called the Reciprocity Model of chord progression. With this aid he looks at some interesting features mainly oriented around the extended meantone fabric of harmony.