The author presents a new interpretation of the Natyasastra (the SRUTI system) of ancient India, showing links with a much older system originating in the nuclear Near-East. The ancient text shows an awareness of the Comma scale (associated with pure intonation). Yet it hides the true structure of this scale in a net of confusing and contradictory information. The author concludes that the artificiality of the system was purposefully presented in order to preserve the truth from the uninitiated.
The author presents a new interpretation of the Natyasastra (the SRUTI system) of ancient India, showing links with a much older system originating in the nuclear Near-East. The ancient text shows an awareness of the Comma scale (associated with pure intonation). Yet it hides the true structure of this scale in a net of confusing and contradictory information. The author concludes that the artificiality of the system was purposefully presented in order to preserve the truth from the uninitiated.
Click on the links to see the articles in your browser or right-click to save the files to your drive.
http://siementerpstra.com/writings/Terpstra-Natyasastra.pdf
http://siementerpstra.com/writings/Terpstra-NatyasastraDiagrams.pdf
 The Pythagorean theory of music was centred around the concept of means. This is understandable, given that all of the ancient Asian cultures saw life as a play of opposites. The Chinese postulated that life is created and balanced through the polarity of the yin-yang. The Babylonians, Egyptians and Greeks also saw life as a dynamically balanced “middle path” between opposites.
The Pythagorean theory of music was centred around the concept of means. This is understandable, given that all of the ancient Asian cultures saw life as a play of opposites. The Chinese postulated that life is created and balanced through the polarity of the yin-yang. The Babylonians, Egyptians and Greeks also saw life as a dynamically balanced “middle path” between opposites. We usually understand the ratios of JI as derived from the Harmonic Series. Any Just interval can be viewed as a frequency ratio between two whole numbers, numbers which refer directly to the Series itself. However, it may not be generally appreciated that there is also an alternative way to generate the Just ratios. This method has great historical importance as well as being of intrinsic interest in itself. I refer to the procedure of examining the
We usually understand the ratios of JI as derived from the Harmonic Series. Any Just interval can be viewed as a frequency ratio between two whole numbers, numbers which refer directly to the Series itself. However, it may not be generally appreciated that there is also an alternative way to generate the Just ratios. This method has great historical importance as well as being of intrinsic interest in itself. I refer to the procedure of examining the  The Tetractys symbol is an exquisite example of how a simple visual pattern can have multi-varied meanings and ‘levels’ of interpretive significance. The famous Pythagorean oath refers to the Tetractys, praising it as the source “which contains the fount and root of eternal nature”. A profusion of insights can be derived from the image, concepts which are relevant to arithmetic (number relations), harmonics (musical tuning theory), and geometry (number relations in space). Only a pitifully small amount of ancient commentary has been perserved; but the study of the above disciplines uncovers more and more relevance for the symbol. In this short paper, I will briefly review some historical interpretations and offer a few insights of my own that come from extensive work in harmonics and sacred geometry.
The Tetractys symbol is an exquisite example of how a simple visual pattern can have multi-varied meanings and ‘levels’ of interpretive significance. The famous Pythagorean oath refers to the Tetractys, praising it as the source “which contains the fount and root of eternal nature”. A profusion of insights can be derived from the image, concepts which are relevant to arithmetic (number relations), harmonics (musical tuning theory), and geometry (number relations in space). Only a pitifully small amount of ancient commentary has been perserved; but the study of the above disciplines uncovers more and more relevance for the symbol. In this short paper, I will briefly review some historical interpretations and offer a few insights of my own that come from extensive work in harmonics and sacred geometry. The two polychords are large steel guitars which were inspired by the ancient chinese instrument called the ch’in or ‘philosopher’s lute’. I wanted an instrument with a long scale length, yet short enough to be playable as a steel guitar (using a sliding bar or ‘steel’). Polychord 1 has two banks of strings; in other words, it is ‘double-necked’. Polychord 2 has a single bank of strings. These two instruments are meant to be together, and to compliment each other. Polychord 1 has a ‘chordal’ tuning; it is a ‘rhythm guitar’ in its orientation. Polychord 2 has a ‘scalar’ tuning; it is a ‘lead’ guitar. This is reflected in the tuning of each instrument.
The two polychords are large steel guitars which were inspired by the ancient chinese instrument called the ch’in or ‘philosopher’s lute’. I wanted an instrument with a long scale length, yet short enough to be playable as a steel guitar (using a sliding bar or ‘steel’). Polychord 1 has two banks of strings; in other words, it is ‘double-necked’. Polychord 2 has a single bank of strings. These two instruments are meant to be together, and to compliment each other. Polychord 1 has a ‘chordal’ tuning; it is a ‘rhythm guitar’ in its orientation. Polychord 2 has a ‘scalar’ tuning; it is a ‘lead’ guitar. This is reflected in the tuning of each instrument. The principle of harmonia – the mediation between extremes through the application of logos or proportion – is the preeminent, central concern of Pythagorean cosmology and philosophy. According to Philolaus (b. c. 470 B.C.E.), the earliest Pythagorean whose fragments have survived, “Nature in the universe was harmonized from Limited and Unlimited elements, both the totality of the kosmos and all the things in it.” Moreover, “Harmonia comes to be in all respects out of contraries; for harmonia is the unity of multiplicity, and the agreement of things that disagree.” The nature of harmonia, the “fitting together” of extremes, was studied by the Pythagoreans on the monochord.
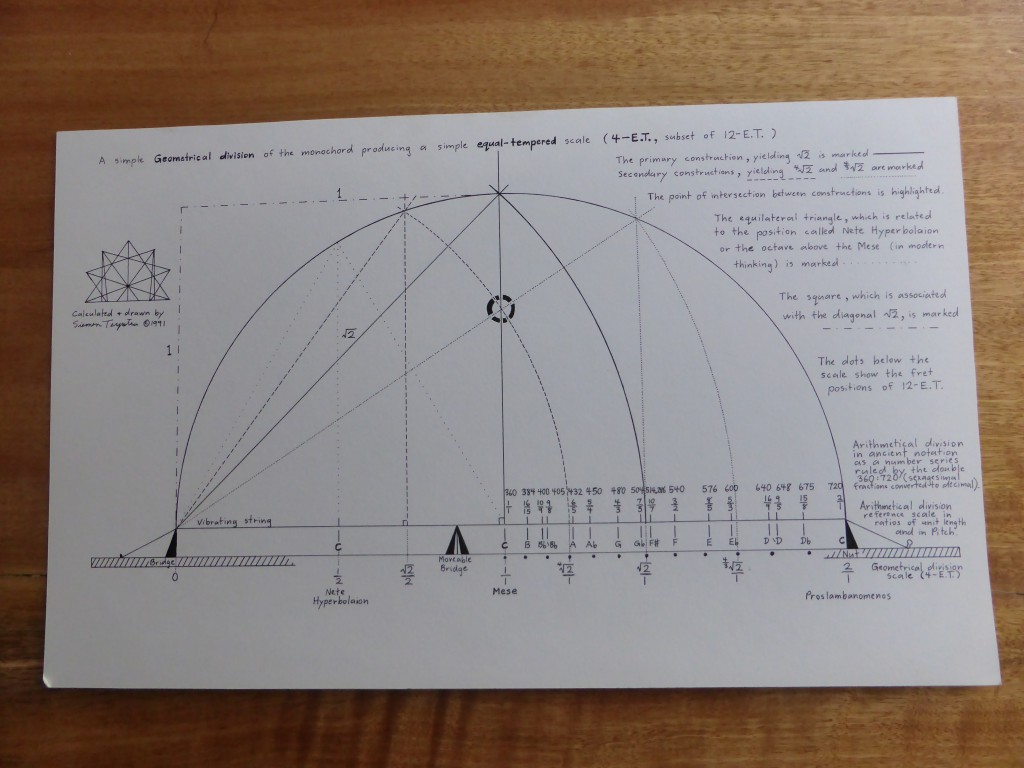
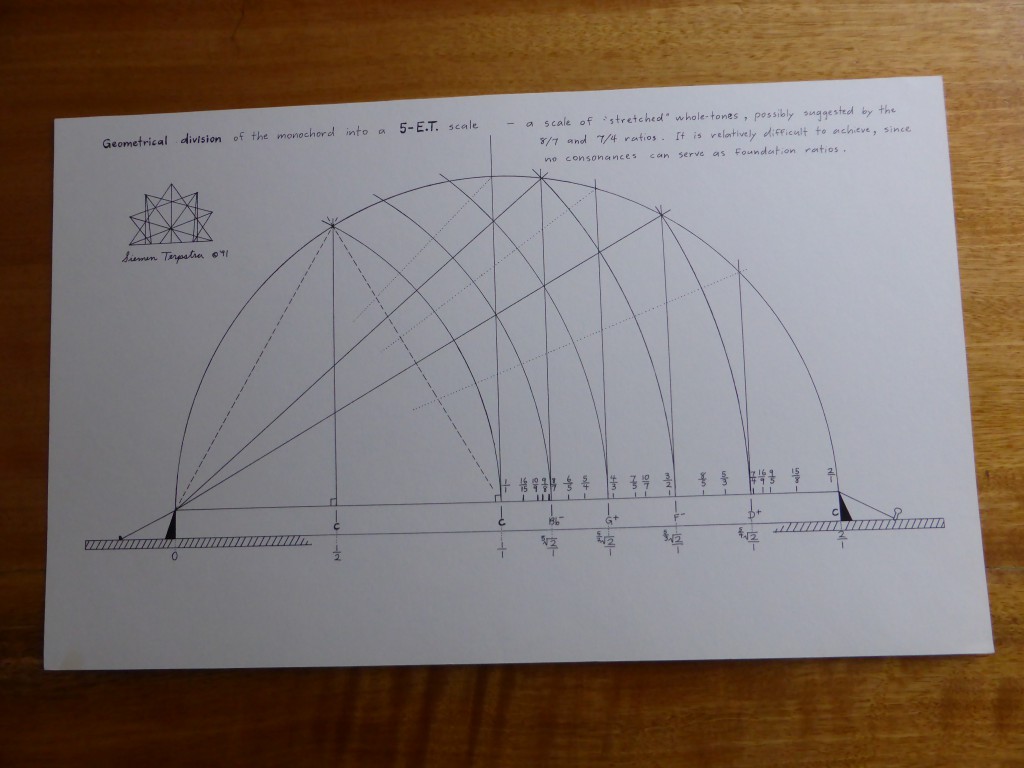
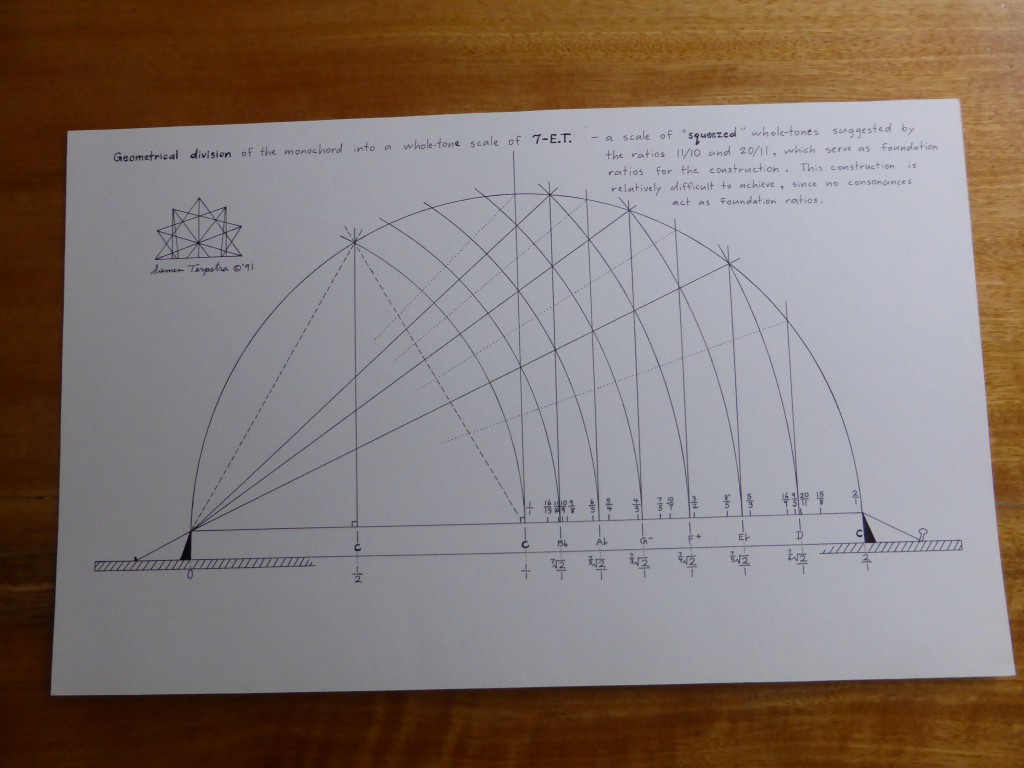
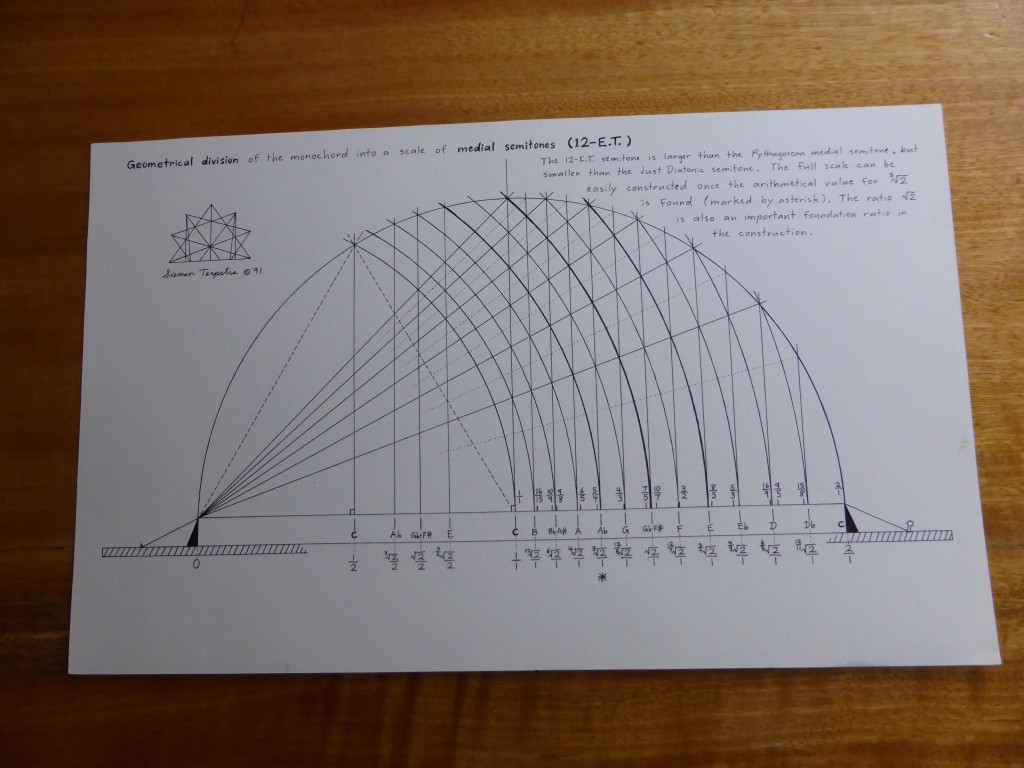
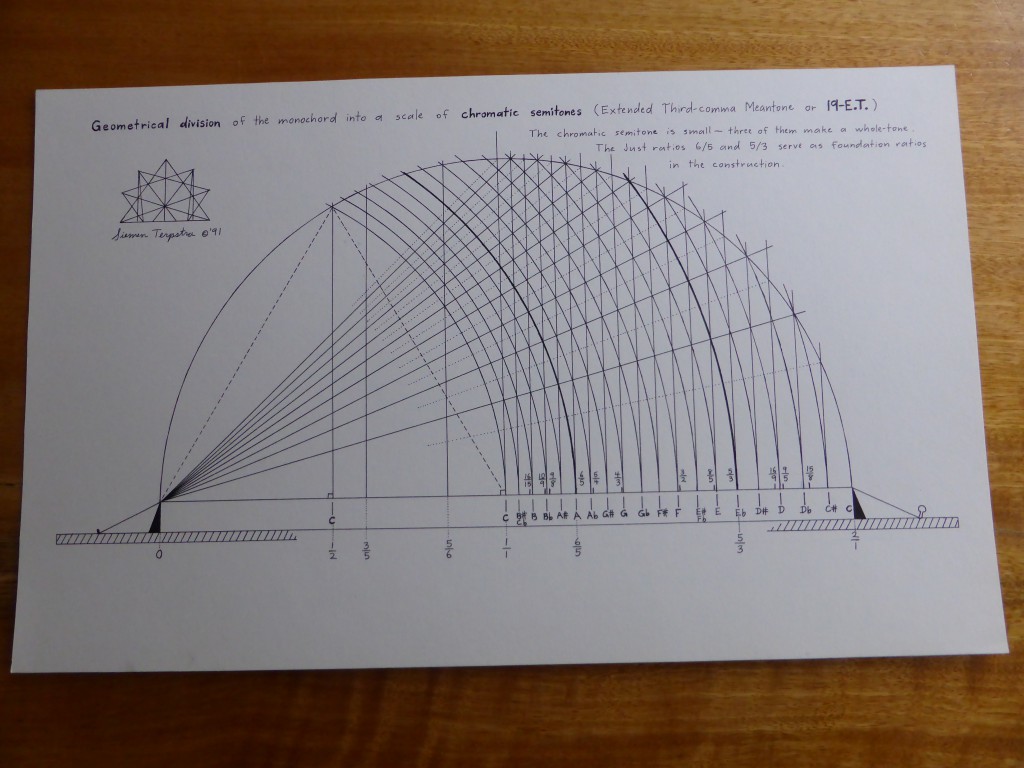
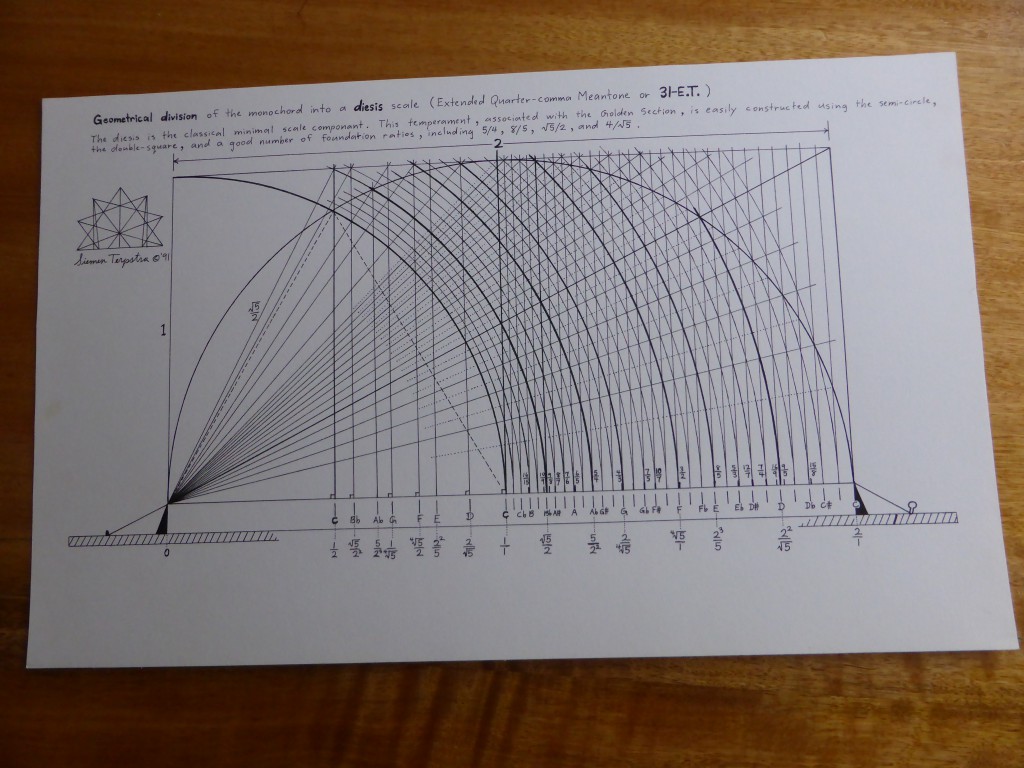
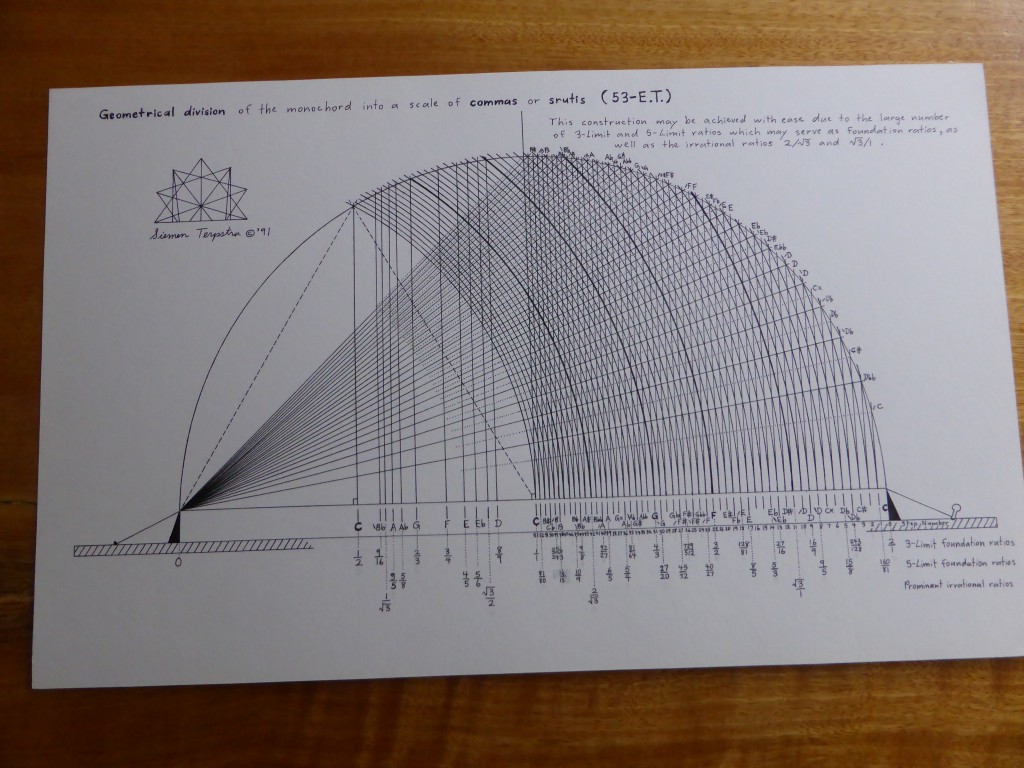
The principle of harmonia – the mediation between extremes through the application of logos or proportion – is the preeminent, central concern of Pythagorean cosmology and philosophy. According to Philolaus (b. c. 470 B.C.E.), the earliest Pythagorean whose fragments have survived, “Nature in the universe was harmonized from Limited and Unlimited elements, both the totality of the kosmos and all the things in it.” Moreover, “Harmonia comes to be in all respects out of contraries; for harmonia is the unity of multiplicity, and the agreement of things that disagree.” The nature of harmonia, the “fitting together” of extremes, was studied by the Pythagoreans on the monochord. The divisions of the monochord string can be represented by four methods: proportional ratios, string lengths, logarithms, and cents. The modern division by cents is derived from the 18th century application of logarithms to music, and cannot be directly applied onto the instruments without further calculation. hence I will only consider ratios and string lengths here. The calibration by string lengths is derivative from the proportional system. It overcomes the cumbersome nature of fractional ratios by clearing fractions through a least common multiple chose as the length of the open string.
The divisions of the monochord string can be represented by four methods: proportional ratios, string lengths, logarithms, and cents. The modern division by cents is derived from the 18th century application of logarithms to music, and cannot be directly applied onto the instruments without further calculation. hence I will only consider ratios and string lengths here. The calibration by string lengths is derivative from the proportional system. It overcomes the cumbersome nature of fractional ratios by clearing fractions through a least common multiple chose as the length of the open string. The author puts together a collection of 3-limit, 5-limit and 7-limit monochord divisions. He lays them out on the matrix and presents both the monochord division and its reciprocal harmonic series component. He emphasizes the invariant zone between the reciprocals.
The author puts together a collection of 3-limit, 5-limit and 7-limit monochord divisions. He lays them out on the matrix and presents both the monochord division and its reciprocal harmonic series component. He emphasizes the invariant zone between the reciprocals. This list of monochord divisions was extracted from my MONOCHORD NUMBERS REFERENCE MATERIAL. In that paper I generated every consecutive just monochord (the series terminating at an arbitrary level of interval complexity) by setting up a strict mathematical rubric. In this paper I selected from this collection the monochords which have the greatest musical and cosmological relevance. I have also presented them in a slightly different manner, in order to bring out the ‘family relations’ between the divisions. It is assumed that the reader of this paper has some familiarity with the monochord concept, and has read my
This list of monochord divisions was extracted from my MONOCHORD NUMBERS REFERENCE MATERIAL. In that paper I generated every consecutive just monochord (the series terminating at an arbitrary level of interval complexity) by setting up a strict mathematical rubric. In this paper I selected from this collection the monochords which have the greatest musical and cosmological relevance. I have also presented them in a slightly different manner, in order to bring out the ‘family relations’ between the divisions. It is assumed that the reader of this paper has some familiarity with the monochord concept, and has read my