I  was repeatedly told that one cannot set a tempered harmony on a monochord by classical means. However, I realised that one exception exists, the complex of multiple divisions 12-et, 24-et, 36-et, 72-et, and 144-et. These very systems are the ones clearly described by Aristoxenus. This realisation prompted the following study of Aristoxenus.
was repeatedly told that one cannot set a tempered harmony on a monochord by classical means. However, I realised that one exception exists, the complex of multiple divisions 12-et, 24-et, 36-et, 72-et, and 144-et. These very systems are the ones clearly described by Aristoxenus. This realisation prompted the following study of Aristoxenus.
I wrote this paper very long ago. I still stand by most of it, but a couple of my conjectures have shifted over the years. In the paper I presumed that Pythagoreans did much of the research into irrational ratios. In spite of the example of Hippasus, I now feel that the Pythagoreans were generally conservatives and the bulwark of anti-temperament sentiment. Work on irrationals was likely done by anti-pythagorean elements, such as Democritus.
Also, I conjecture that Philolaus the Pythagorean supports 53-et. Now I no longer believe that to be the case. My argument there was simple enough. Since he knew that the 8:9 whole tone is nine commas in size, he must have known that the ditone equals eighteen commas, the fourth twenty-two and the octave fifty-three. He may well have thought that his commas were all the same size, when they were likely not to be so. I now think that Philolaus probably abhorred the very idea of temperament.
For my current thinking on this topic, see my recent essay HOMAGE TO PTOLEMY (a companion paper to ARISTOXENUS) under the heading MONOCHORD. See also RESTORING THE MUSE under the philosophy heading.
Click on the links to see the article in your browser or right-click to save the files to your drive.
http://siementerpstra.com/writings/Terpstra-Aristoxenus.pdf
http://siementerpstra.com/writings/Terpstra-AristoxenusDiagrams.pdf

 The author re-examines the syntax of Gesualdo’s musical style in the light of the intonational practices of his time. A theoretical structure with which to describe his harmonic practices, and those of other 16th Century composers, is developed. The historical context is presented as well as a series of analyses of Gesualdo’s music.
The author re-examines the syntax of Gesualdo’s musical style in the light of the intonational practices of his time. A theoretical structure with which to describe his harmonic practices, and those of other 16th Century composers, is developed. The historical context is presented as well as a series of analyses of Gesualdo’s music. The author develops a syntax for meantone harmony based on the structural characteristics of the temperament. These features include a description of the Regions with their boundary functions, and also the three genera. An abstract topology of triad progression is introduced, as well as an introduction to the organization of functional tables for 31-ET.
The author develops a syntax for meantone harmony based on the structural characteristics of the temperament. These features include a description of the Regions with their boundary functions, and also the three genera. An abstract topology of triad progression is introduced, as well as an introduction to the organization of functional tables for 31-ET. The purpose of this article is to examine certain aspects of theory which concert practical musical composition in 31-E.T. (or extended meantone). The principles which are put forth may also be used to advantage with other equal divisions, including 12-E.T., 19-E.T., and so on. This article was meant to compliment the other articles which I have written on meantone theory. Those articles are:
The purpose of this article is to examine certain aspects of theory which concert practical musical composition in 31-E.T. (or extended meantone). The principles which are put forth may also be used to advantage with other equal divisions, including 12-E.T., 19-E.T., and so on. This article was meant to compliment the other articles which I have written on meantone theory. Those articles are:  Some representative examples of symmetrical structures are presented, along with a comparison between the types of symmetry in 31-E.T. and other equal-tempered systems. The Euler-Fokker genera are interpreted as a means of generating symmetrical structures. Lastly, an alternative method of generating the most important symmetrical functions is outlined.
Some representative examples of symmetrical structures are presented, along with a comparison between the types of symmetry in 31-E.T. and other equal-tempered systems. The Euler-Fokker genera are interpreted as a means of generating symmetrical structures. Lastly, an alternative method of generating the most important symmetrical functions is outlined. This collection of harmonies is an expansion of the set presented in my paper
This collection of harmonies is an expansion of the set presented in my paper  The author explains how tendencies within the structure of the Pythagorean chromatic scale supported the transfer to Just Intonation; however, certain features of Just Intonation necessitated the application of some form of temperament. The meantone temperament formed the best compromise for the musical styles that were being explored. The author aims at a co-relation between tuning paradigm and associated musical style.
The author explains how tendencies within the structure of the Pythagorean chromatic scale supported the transfer to Just Intonation; however, certain features of Just Intonation necessitated the application of some form of temperament. The meantone temperament formed the best compromise for the musical styles that were being explored. The author aims at a co-relation between tuning paradigm and associated musical style.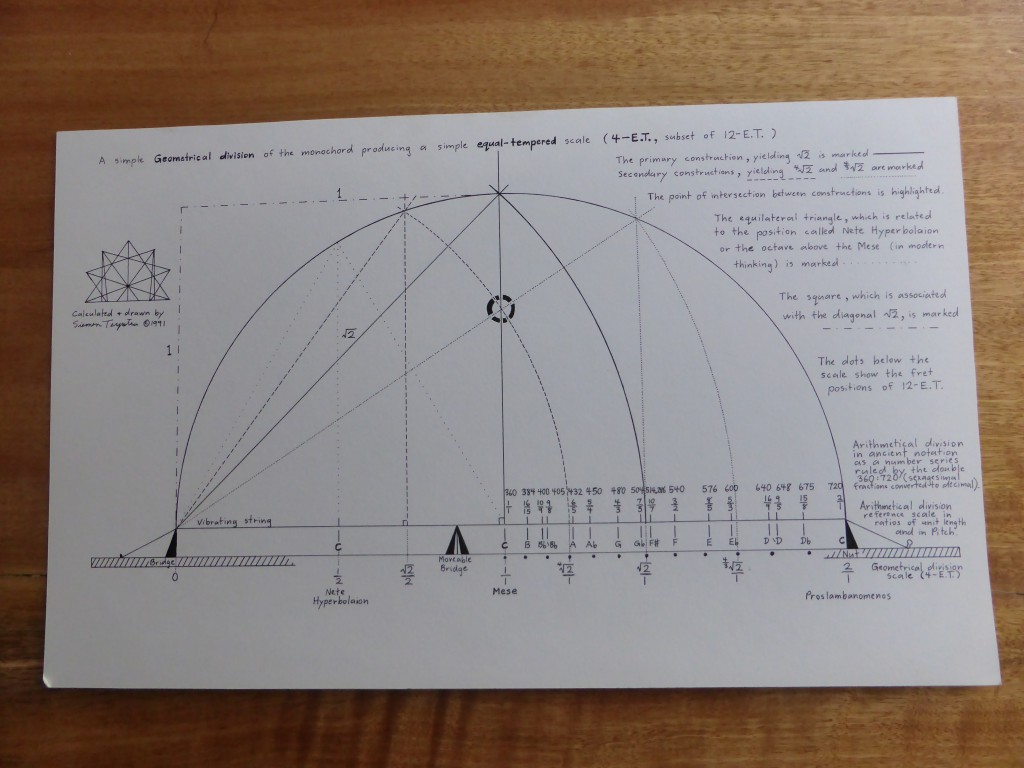
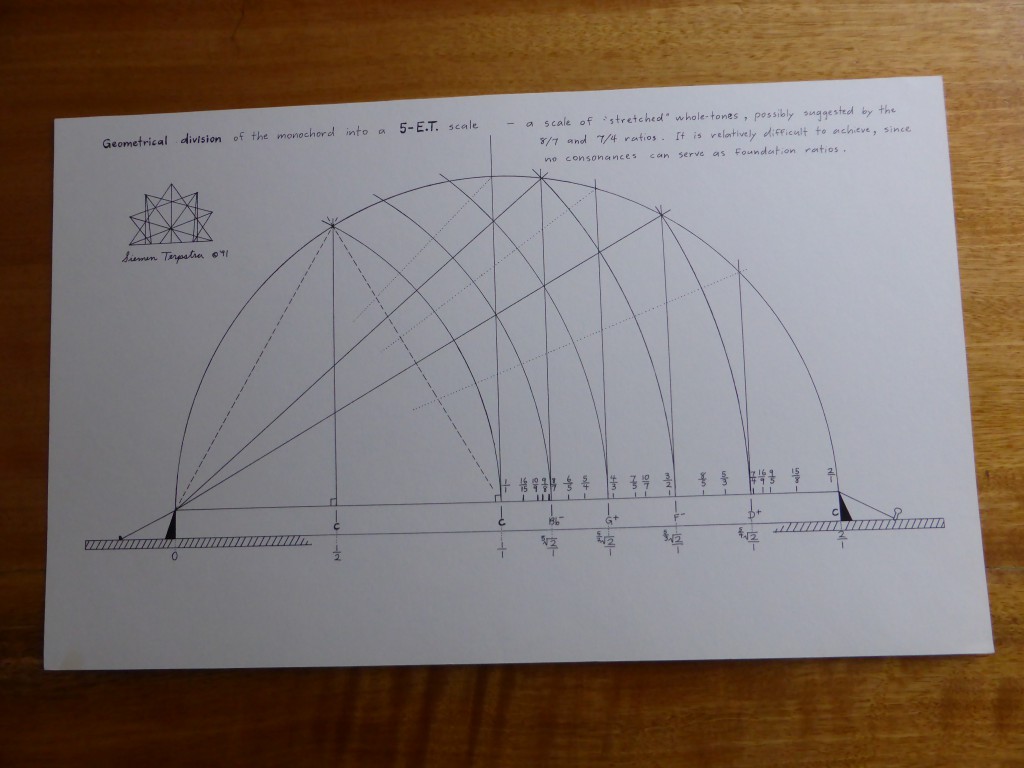
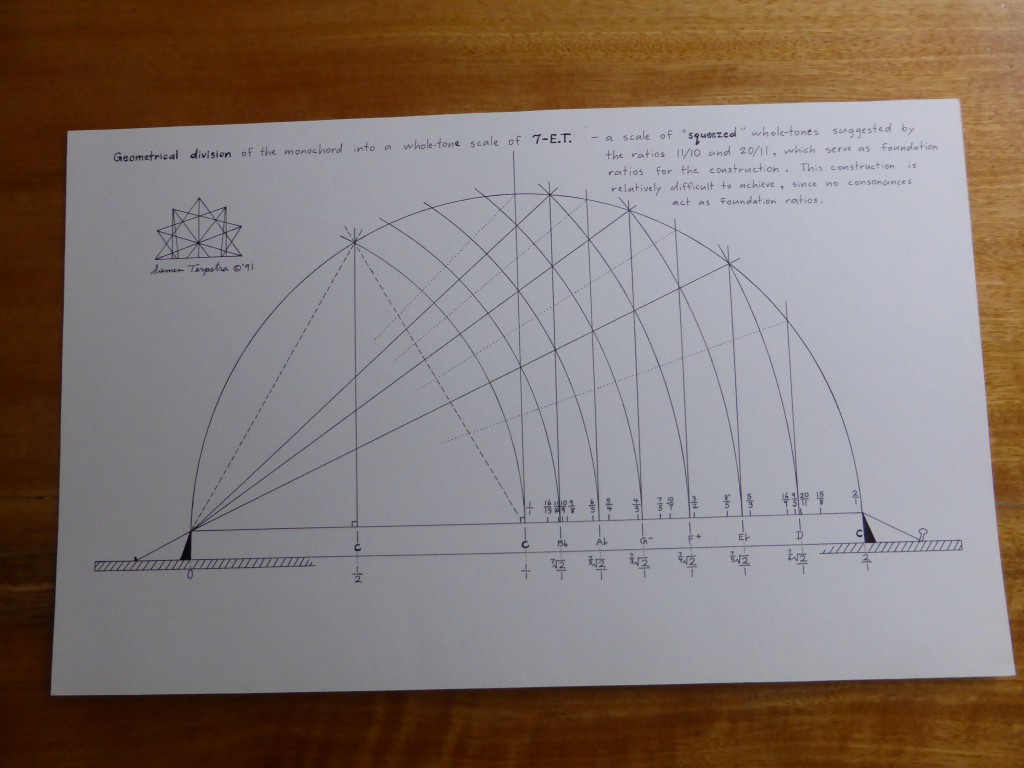
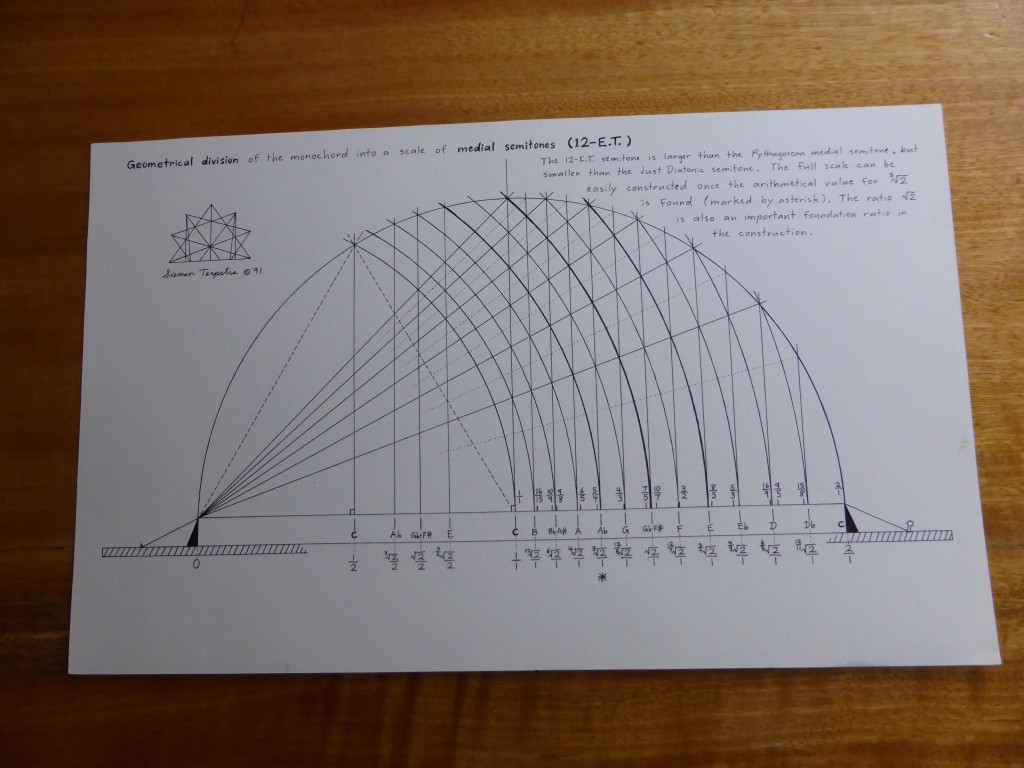
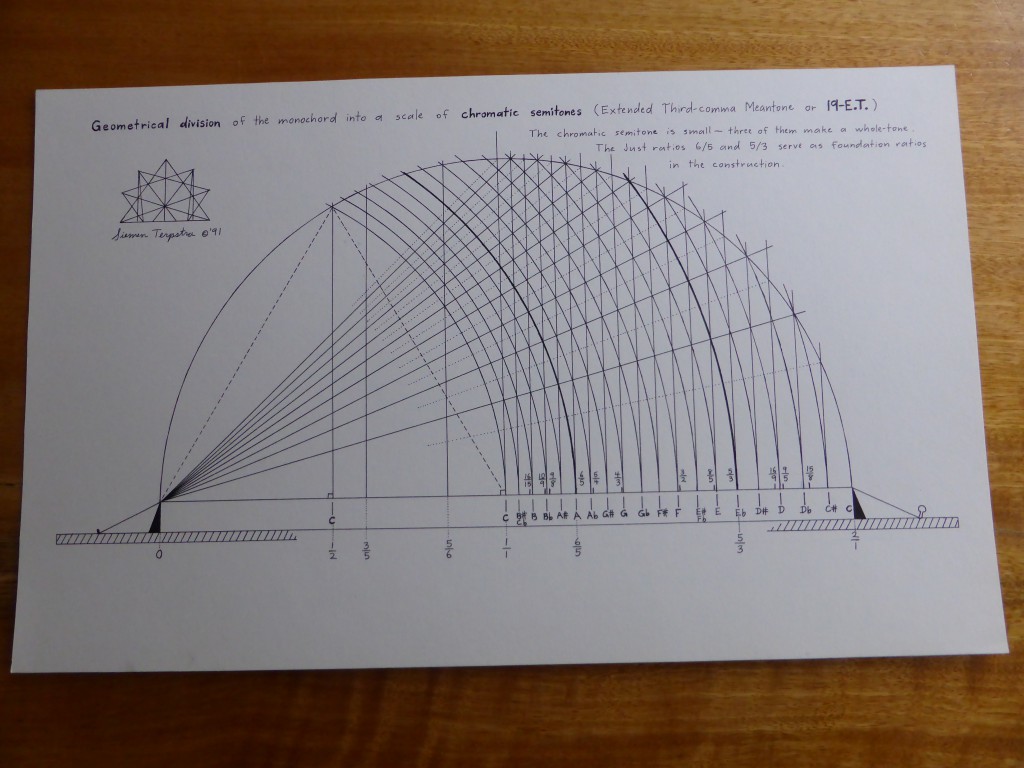
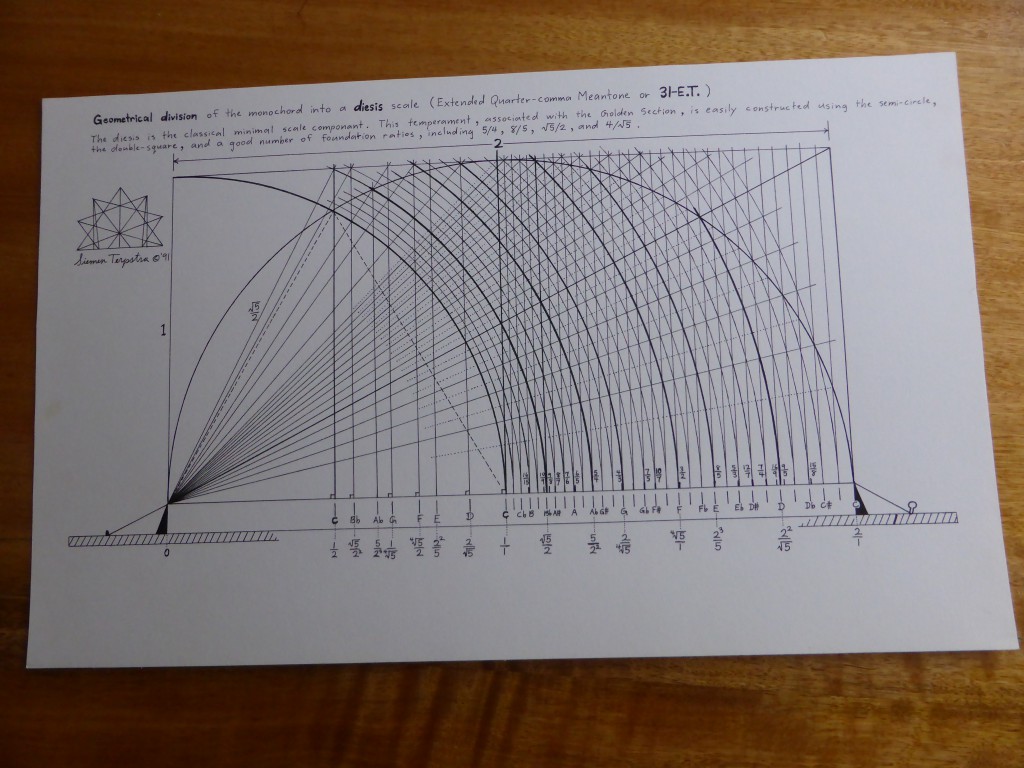
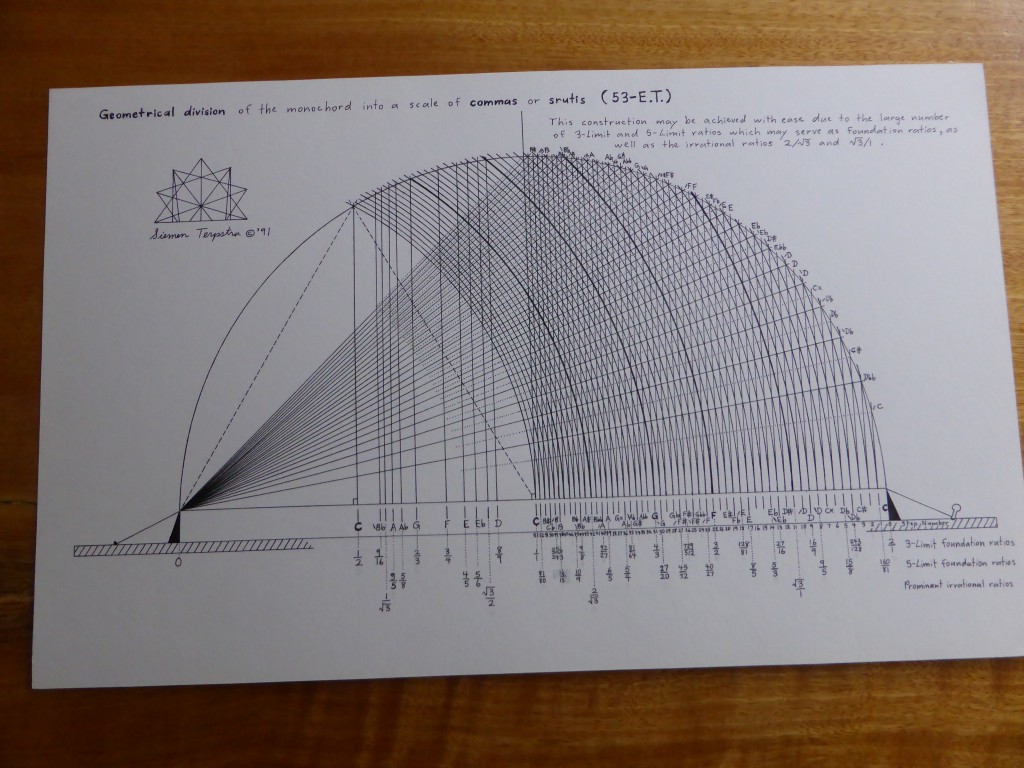
 was repeatedly told that one cannot set a tempered harmony on a monochord by classical means. However, I realised that one exception exists, the complex of multiple divisions 12-et, 24-et, 36-et, 72-et, and 144-et. These very systems are the ones clearly described by Aristoxenus. This realisation prompted the following study of Aristoxenus.
was repeatedly told that one cannot set a tempered harmony on a monochord by classical means. However, I realised that one exception exists, the complex of multiple divisions 12-et, 24-et, 36-et, 72-et, and 144-et. These very systems are the ones clearly described by Aristoxenus. This realisation prompted the following study of Aristoxenus. The author presents an analysis of the structure of irregular temperaments, with special emphasis on well-temperaments or circulating temperaments. Roughly 200 scales are examined, of which about a third are historical and the rest are original to the author. A systematic method is presented for the conversion of various regular temperaments (meantone temperaments) into circulating temperaments. Thus the historical material is embedded within the wider context of scalar architecture. The aim is an overview, leading to the understanding and control of design characteristics.
The author presents an analysis of the structure of irregular temperaments, with special emphasis on well-temperaments or circulating temperaments. Roughly 200 scales are examined, of which about a third are historical and the rest are original to the author. A systematic method is presented for the conversion of various regular temperaments (meantone temperaments) into circulating temperaments. Thus the historical material is embedded within the wider context of scalar architecture. The aim is an overview, leading to the understanding and control of design characteristics.